Ante la pregunta que se nos plantea hemos decidido indagar en diversas fuentes de información para llegar a conocer lo que otras personas piensan sobre el tema.Para ello hemos realizado una entrevista a niños de diferentes edades, los cuales han respondido de la siguiente manera:
“Claro que sirven para la vida. Sirven para sumar y porque nos enseñan los números. Si no yo no sabría que una cosa cuesta por ejemplo cien pesetas”. Rosa (6º de Primaria).
“No, no valen pa´ na´ . Yo eso de las fracciones no me entero. Un cuarto, tres doceavos, me voy a comer un octavo de tarta. Yo no digo un octavo. ¡Yo digo un TROZO DE TARTA!.” Lola. (4º de Primaria)
“Si, si valen. Aunque yo cuando voy a comprar cuento con los dedos y por duros. Esto un duro y dos duros, tres duros. ¿Tres duros y son...15 pesetas?. Pero eso yo lo hago con mi cabeza no con las matemáticas. Con cuentas y todo eso.” Antonio (3º de Primaria)
“Pero eso son cuentas. Cuentas mentales. ¡Claro que valen!. Tu vas a un sitio y no te engañan si sabes matemáticas. A mi abuela la engañan y a mi no.” María (6º de Primaria)
“Si lo de los números y sumar si vale. Pero ¿para qué valen las raíces cuadradas?. Mira, quiero la raíz cuadrada de 81 chicles... y te mandan a la mierda.” Pedro (6º de Primaria)
“Si y yo que estoy dando las potencias. Quiero 34 chicles. ¿Cuánto es 34? 81.¡¡Vale, vale, quiero 34 chicles!!.” Araceli (6º de Primaria)
De estas anotaciones creemos relevante resaltar que;
 Es evidente que los niños consideran como dos campos distintos e inconexos: las matemáticas escolares, entendidas de forma científica, y las matemáticas de la vida cotidiana.
Es evidente que los niños consideran como dos campos distintos e inconexos: las matemáticas escolares, entendidas de forma científica, y las matemáticas de la vida cotidiana. Algunos contenidos matemáticos son reconocidos fácilmente aplicados a la práctica, mientras que otros se prestan menos al reconocimiento o toma de conciencia.
Algunos contenidos matemáticos son reconocidos fácilmente aplicados a la práctica, mientras que otros se prestan menos al reconocimiento o toma de conciencia. La motivación es mayor si le encuentran funcionalidad a los contenidos matemáticos en su contexto inmediato. Por lo tanto, sería recomendable crear en los niños la necesidad de acudir a la matemática para encontrar solución a los problemas cotidianos.
La motivación es mayor si le encuentran funcionalidad a los contenidos matemáticos en su contexto inmediato. Por lo tanto, sería recomendable crear en los niños la necesidad de acudir a la matemática para encontrar solución a los problemas cotidianos. Sería necesario replantear la secuenciación de los contenidos matemáticos en función de la realidad y características contextuales. Evitando la parcelación en cuanto a su tratamiento y apostando por su encadenamiento significativo (es decir, unos contenidos lleven a otros, se parta de lo asimilado por los niños antes de comenzar a trabajar un nuevo aspecto matemático,...).
Sería necesario replantear la secuenciación de los contenidos matemáticos en función de la realidad y características contextuales. Evitando la parcelación en cuanto a su tratamiento y apostando por su encadenamiento significativo (es decir, unos contenidos lleven a otros, se parta de lo asimilado por los niños antes de comenzar a trabajar un nuevo aspecto matemático,...).Todas estas ideas van a repercutir en la práctica educativa.
Al respecto otros autores aportan ...
... Interesantes reflexiones sobre el tema que nos ocupa:
Kamii, por ejemplo, exalta la necesidad de aportar conocimientos sobre la realidad a partir de la cual el niño construirá su conocimiento, estableciéndose necesario modificar la planificación de un día típico en el porqué y en el cómo, haciendo hincapié en las actividades de conocimiento físico y en los juegos de grupo.
Vasco distingue que el fallo de la matemática moderna se debe a la falta de similitud entre el sistema conceptual de los profesores y el de los autores de los libros de texto, y el sistema conceptual de los niños. Hecho que contradice lo que la LOGSE (1/1990 del 3 de Octubre) regula; promulgando que “el área de matemáticas acoge un valor funcional como conjunto de procedimientos para resolver problemas en diversos campos, para poner de relieve aspectos y relaciones de la realidad y para anticipar y predecir hechos y situaciones o resultados antes de que se produzcan o se observen”.
Podemos destacar la línea común de todas estas aportaciones: la necesidad de facilitar la relación entre matemáticas escolares y cotidianas.
Si existen, pero...
Cuando seamos capaces de construir un puente entre las matemáticas y la vida diaria conseguiremos ser conscientes de esta existencia.
Algunas de las vías para llegar a esta construcción son, entre otras:
 técnica role play: dramatizaciones en clase de situaciones de la vida cotidiana en las que sea necesaria la práctica matemática.
técnica role play: dramatizaciones en clase de situaciones de la vida cotidiana en las que sea necesaria la práctica matemática. Responsabilidades matemáticas: administración de materia, creación de comisiones para reparto de tareas, gestión para viaje de fin de curso,...
Responsabilidades matemáticas: administración de materia, creación de comisiones para reparto de tareas, gestión para viaje de fin de curso,... Partir de las aportaciones que hacen los niños de cómo relacionan las matemáticas de la vida cotidiana en la escuela.
Partir de las aportaciones que hacen los niños de cómo relacionan las matemáticas de la vida cotidiana en la escuela.
Publicado por: Pierina Aguilar


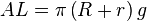
![A = \pi \left[(R + r\right)g + R^2 + r^2]](http://upload.wikimedia.org/math/8/a/e/8ae44a33923b3a0e58bbd584d6cee0c9.png)

 En una determinada casa las dos alas del tejado tienen diferente inclinación; una ala tiene una inclinación de 60º y la otra de 70º. Supongamos que un gallo pone un huevo exactamente en la cumbre. ¿Hacia quá lado del tejado caería el huevo?
En una determinada casa las dos alas del tejado tienen diferente inclinación; una ala tiene una inclinación de 60º y la otra de 70º. Supongamos que un gallo pone un huevo exactamente en la cumbre. ¿Hacia quá lado del tejado caería el huevo?  En una línea de ferrocaril, el tendido tiene doble vía excepto en un túnel, que no es lo bastante ancho para acomodar ambas. Por ello, en el túnel, la línea es de vía simple. Una tarde, entró un ten en el túnel marchando en un sentido, y otro tren en el mismo túnel, pero en sentido contrario. Ambos iban a toda velocidad; y sin embargo no llegaron a colisionar. Explíquelo.
En una línea de ferrocaril, el tendido tiene doble vía excepto en un túnel, que no es lo bastante ancho para acomodar ambas. Por ello, en el túnel, la línea es de vía simple. Una tarde, entró un ten en el túnel marchando en un sentido, y otro tren en el mismo túnel, pero en sentido contrario. Ambos iban a toda velocidad; y sin embargo no llegaron a colisionar. Explíquelo. En el espacio aéreo se cruzan un avión comercial y un caza militar. Con estos datos, ¿podemos saber cómo se hablan los pilotos?
En el espacio aéreo se cruzan un avión comercial y un caza militar. Con estos datos, ¿podemos saber cómo se hablan los pilotos?