Hola a Todos:
Bueno como mucha gente no sabia la explicacion matematica del porque en el cuadrado del examen el area aumentaba cuando se cambiaban de posiciones las piezas; la encontre por ahi en internet y ahora la comparto con ustedes...
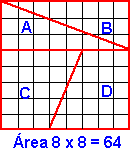
- Dibuja en un papel o cartulina un cuadrado de 8 x 8
- Recorta los dos triángulos y los dos trapecios como se indica en la figura.
- Coloca las piezas de modo que formen un rectangulo
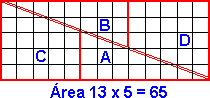
- Resulta un rectángulo de lados: largo = 13 cm., ancho = 5 cm.
- Como el rectangulo se compone de las mismas piezas que el cuadrado, deberian tener la misma área; Sin embargo...
Área del cuadrado: 8 cm. x 8 cm. = 64 cm2
Área del rectángulo:13 cm. x 5 cm. = 65 cm2
PERO...
¿A que se debe la diferencia de 1 cm2 ?
En realidad, entre el rectángulo de lados 13 cm y 5 cm y el construido con las piezas A, B, C y D queda un pequeño espacio, imposible de detectar a simple vista, de 1 mm de ancho y que en total tiene 1 cm2, que es la diferencia entre las áreas
.
.
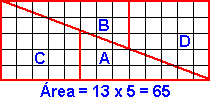
Las sorpresas de este tipo se llaman paradojas de Hooper, porque este autor las presentó en su obra Rational Recreations en 1795
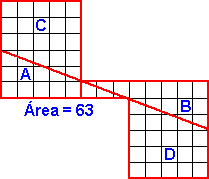
Sam Lloyd mostró ingeniosamente que las piezas pueden disponerse de forma que aparentemente sea 8 x 8 = 63:
¿Interesante no?
Encontre en la red otras paradojas matematicas que me parecieron mas interesantes que esta, pero las dejare para mi proximo post...
Hablamos xD
Publicado por: Jose Pohl
Muy buena pagina :D
ResponderEliminarLOCASO! no sabia que también reducía en otra posición :)
ResponderEliminarAndrea Garrido 4B
En mi opinión la respuesta arriba es falsa, ilusoria. El problema no empieza con el cuadrado de 8 x 8 si no en el rectángulo de 13 x 5, particionado en 4 rectángulos, de los cuales dos se convierten en 4 triángulos, uno queda como está, 5 x 3 y el último de 8 x 2 se convierte en otro cuadrado de 5 x 3. Es decir, la presentacion empieza con un cm2 de menos en un rectangulo de 13 x 5 con un cm2 menos. Salud!
ResponderEliminar